세리프 따라잡기
WEEK02 - TIL 시간 복잡도(basic) 본문
알고리즘 스피드는 완료까지 걸리는 절차의 수로 결정이 된다.
→ 따라서 같은 작업을 수행하는데 5단계만 수행하면 되는 알고리즘이 10단계를 수행하는 알고리즘보다 좋은 알고리즘이다.
1. 상수 시간(constant time)
ex. 선형 탐색 알고리즘은 1개씩 차례대로 다 검사를 해보는데, 만약 데이터가 무수히 많다면...........? 무수히 많은 단계를 거쳐야 한다~ [ n=input()이라면 n단계를 거쳐야 함 ]
→ 선형 탐색은 O(N)의 시간 복잡도를 가짐

빠르다/느리다 라고 표현하는 것보다 더 직관적으로 빠르게 설명할 수 있다 == BigO
BigO를 이해한다면? = 알고리즘 분석을 더 빠르게 할 수 있고, 언제 무엇을 쓸지 파악이 가능하며, 자신의 코드를 평가할 수 있다. (이 코드가 미래에 어떻게 작동할지 알 수 있기 때문!)
ex.
def print_first(arr):
print(arr[0])위의 코드가 10번 실행해도 딱 1번의 실행이면 끝날 것이고, 100번이어도 1번에 끝날 것!
= 이 함수는 동일한 수의 단계만이 필요하기 때문에. 이 함수의 시간복잡도는 상수 시간(constant time)이라고 한다
→ 왜냐? n이 얼마나 큰 지 상관없이 수행을 끝내는데 동일한 숫자의 단계만 필요하기 때문

위 코드를 BigO에서는 O(1)이라고 표현한다.
def print_first(arr):
print(arr[0])
print(arr[0])아까의 함수에서 arr[0]을 2번 print한다면, 딱 보았을 때 이번엔 2단계가 필요한 것 같지만!! ( like: O(2) )
여전히 동일하게 O(1)이다~~ 왜냐하면 BigO는 디테일에는 관심이 없다(고 한다😮) - 큰 원리에만 관심이 있다고..!
그래서 이 함수의 input이 거대해져도, BigO는 미리 정해진 숫자에 따라 작동한다. (BigO를 이해하려면 기억!!)
→ 상수(constant)에는 전혀 신경을 쓰지 않는다.
ex)ex. 위 코드가 이후 200까지 늘어나도, input 사이즈와 관계없이 여전히 O(1)라는 것
== 여전히 constant time(일정한 시간/상수)이기 때문에!
∴ 즉, 상수 시간 알고리즘은 input 사이즈와 관계없이 스텝이 정해진 알고리즘을 말하며 항상 선호되는 알고리즘이다. (하지만 항상 이렇게 만들긴 힘들다~)
ex.
def print_all(arr):
for n in arr:
print(n)각 아이템을 다 프린트하는 함수, 배열이 10개라면 10번을, 배열이 100개라면 100번의 단계가 있는데 == 선형 탐색과 비슷하다. (배열의 각각 아이템을 위해 모두 작업해야해서)
→ 배열이 커지면, 필요한 단계 또한 커진다. BigO에선 이걸 O(N)이라고 한다. (상수는 관계 없다!!)
def print_all(arr):
for n in arr:
print(n)
for n in arr:
print(n)이렇게 함수를 반복하면 이론적으론 O(2N)이 되어야 할 것 같지만~ 이건 상수기 때문에 여전히 O(N)으로 표현!
→ 핵심은 바뀌지 않기 때문이다! [input이 증가하면 단계가 증가한다는 것이 핵심= 선형적으로 증가]
2. Quadratic Time(2차 시간)
= 중첩 반복(Nested Loops)이 있을 때 발생
ex.
def print_twice(arr):
for n in arr:
for x in arr:
print(x,n)이 함수는 배열의 각 아이템에 대해 루프를 반복해 실행. 따라서 시간복잡도는 input의 n²인 것.
→ 만약 input이 10개라면, 완성하는데 100단계가 필요한 것. 왜냐면 루프 안의 루프에서 함수를 실행하기 때문!

'선형 탐색(O(N))'과 '2차 시간(O(N²)'을 비교하면 선형의 시간복잡도가 더 효율적인 것으로, 선호된다.
3. 로그 시간(Logarithmic time)
= 이진 탐색 알고리즘 설명할 때 쓰이는 것
이진 검색에서는 input 사이즈가 더블(10>20)이 되어도 단계는 단 1개 밖에 증가하지 않는다.
→ 이진 탐색에서는 각 과정의 단계를 절반으로 나눠서 진행하기 때문이다. == O(logN)
→→ 한 번만 더 나누면 되는 것이니까.
로그(logarithm)는 지수(exponent)의 정반대
지수 : Q: 2ⁿ=32 일때 n은 몇인가? / A. 5
로그 : Q: n = log₂32 일때 n은 몇인가?
A. (몇 번을 나누어야 32를 2로 몇 번을 나눠야 1이 나올까?) 32/2, 16/2, 8/2, 4/2, 2/2 = 총 5번
→ 이 과정이 이진 탐색과 비슷하다.

∴ 이진 검색의 시간복잡도는 O(logN)
※ 이진 검색은 정렬되지 않은 배열엔 사용할 수 없다!
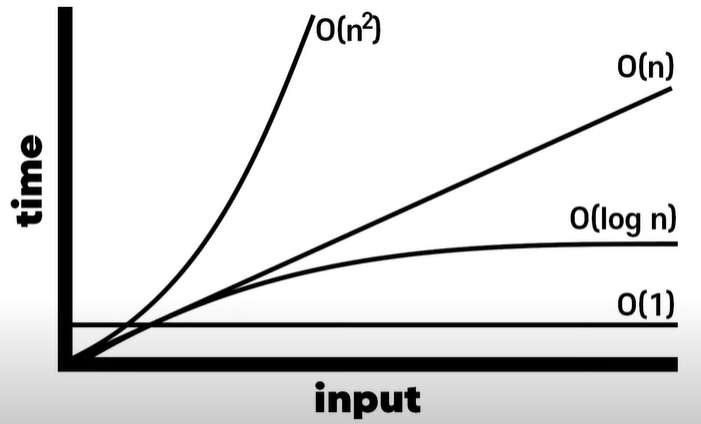
★☆요약!☆★
(시간 복잡도 느림) 지수시간, 이차 시간 > 선형 탐색 > 이진 탐색 > 상수 시간 (빠름)
'SW사관학교 정글' 카테고리의 다른 글
| WEEK03- TIL DFS와 BFS (0) | 2022.04.16 |
|---|---|
| WEEK03- TIL 최소 스패닝 트리 (0) | 2022.04.15 |
| WEEK02 - TIL 우선순위 큐(Priority Queue) (0) | 2022.04.11 |
| WEEK02 - TIL 스택/큐 (0) | 2022.04.10 |
| WEEK02- TIL 분할정복 (0) | 2022.04.09 |



